Loading...
مدل سازی آونگ فوکو (Foucault Pendulum) در Simulink متلب
در این مقاله آموزشی متلب مثال پیش رو نحوه مدل سازی آونگ فوکو (Foucault Pendulum) در محیط سیمولینک MATLAB را نشان می دهد. آونگ فوکو زاییده فکر لئون فوکو فیزیک دان فرانسوی بود. هدف آن اثبات این بود که زمین به دور محور خود می چرخد. صفحه نوسان آونگ فوکو در طول روز در نتیجه چرخش محوری زمین می چرخد. صفحه نوسان یک دایره کامل را در بازه زمانی T تکمیل می کند که به عرض جغرافیایی بستگی دارد. معروف ترین آونگ فوکو در داخل پانتئون پاریس نصب شد. این یک کره فلزی 28 کیلو گرمی بود که به سیمی به طول 67 متر متصل شده بود. این مثال نیز یک آونگ به طول 67 متر در عرض جغرافیایی پاریس را شبیه سازی می کند.
مدل Simulink
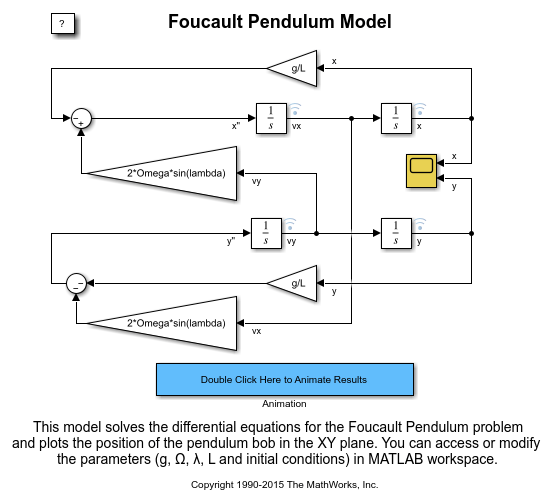
ساده ترین راه برای حل مسئله آونگ فوکو در سیمولینک MATLAB ساختن مدلی است که معادلات دیفرانسیل کوپل شده (ODE) را برای سیستم حل کند. این مدل در شکل سیمولینک زیر نشان داده شده است. معادلاتی که آونگ فوکو را توصیف می کند در زیر آورده شده است. برای جزئیات در مورد فیزیک مدل و استخراج این معادلات، به بخش تجزیه و تحلیل و فیزیک که در ادامه همین آموزش ارائه شده مراجعه کنید.
باز کردن مدل
در پنجره فرمان متلب sldemo_foucault را تایپ کنید تا این مدل باز شود.
1 | openExample('simulink_general/sldemo_foucaultExample') |
این مدل داده های شبیه سازی را در متغیر sldemo_foucault_output ثبت می کند. سیگنال های ثبت شده دارای نشانگر آبی هستند. برای اطلاعات بیشتر، مقاله پیکربندی سیگنال برای ورود به سیستم را ببینید.
شرایط اولیه
این مدل ثابت ها و شرایط اولیه را از فایل sldemo_foucault_data.m بارگذاری می کند. محتویات این فایل در جدول زیر نشان داده شده است. شما می توانید پارامترهای شبیه سازی را مستقیما در فضای کاری متلب تغییر دهید. دامنه اولیه آونگ باید در مقایسه با طول آونگ کوچک باشد، زیرا معادلات دیفرانسیل فقط برای نوسانات کوچک معتبر است.
جدول مدل آونگ فوکو
اجرای شبیه سازی
دکمه Play را در نوار ابزار در پنجره مدل فشار دهید تا شبیه سازی اجرا شود. شبیه سازی از یک متغیر حل کننده stiff و ode23t استفاده می کند. این یک آونگ فوکو را به مدت 3600 ثانیه شبیه سازی می کند (شما می توانید زمان شبیه سازی را تغییر دهید). همچنین این مدل از یک تحمل نسبی پیش فرض RelTol = 1e-6 استفاده می کند.
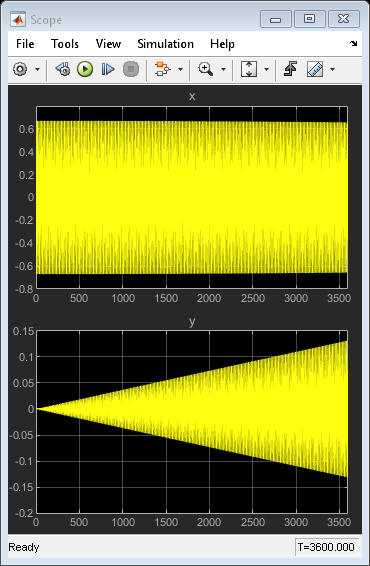
شکل نتایج شبیه سازی آونگ فوکو (زمان شبیه سازی 3600 ثانیه)
نتایج شبیه سازی
نتایج شبیه سازی در شکل بالا نشان داده شده است. شبیه سازی مختصات x و y پاندول و مولفه های سرعت x و y آونگ را محاسبه می کند. صفحه نوسانات آونگ ۳۶۰ درجه را در بیش از ۲۴ ساعت کامل می کند. این دوره تابعی از عرض جغرافیایی لامبدا است (به بخش مشتق در تجزیه و تحلیل و فیزیک در ادامه این مقاله آموزشی مراجعه کنید).
شکل بلوک انیمیشن که نشان می دهد صفحه نوسان آونگ در یک ساعت چقدر می چرخد
پس از اجرای شبیه سازی، روی بلوک انیمیشن دابل کلیک کنید تا نتایج متحرک شوند.
توجه: بخش Animate Results از مثال به جعبه ابزار پردازش سیگنال (Signal Processing Toolbox) نیاز دارد. در صورتی که تولباکس پردازش سیگنال بر روی متلب شما نصب نباشد، دابل کلیک کردن روی بلوک انیمیشن با خطا مواجه می شود. تمام قسمت های دیگر مثال، بدون نیاز به تولباکس Signal Processing به درستی کار می کنند.
فایل sldemo_foucault_animate.m نشان می دهد که موقعیت آونگ در نقاط مختلف در زمان تغییر می کند. شما می توانید به روشنی ببینید که چگونه صفحه نوسان آونگ می چرخد.
توجه: اگر شبیه سازی را با تلورانس نسبی زیاد اجرا کنید، نتیجه از نظر عددی در یک دوره زمانی طولانی ناپایدار خواهد بود. مطمئن شوید که از متغیر حل کننده stiff استفاده می کنید. در مثال حل کننده های مرحله ای متغیر با استفاده از مدل Stiff درباره ناپایداری عددی مسائل سخت و عملکرد حل کننده بیشتر بخوانید. این مثل با اجرای دستور زیر در پنجره فرمان متلب قابل اجرا و بررسی است:
1 | showExample('simulink_general/sldemo_solversExample') |
بستن مدل
مدل را ببندید و داده های تولید شده را پاک کنید.
تجزیه و تحلیل و فیزیک
این بخش آونگ فوکو را تحلیل می کند و فیزیک پشت آن را تشریح می کند. آونگ را می توان به عنوان یک جرم نقطه ای معلق روی سیمی به طول L مدل کرد. آونگ در عرض جغرافیایی لامبدا قرار دارد. استفاده از چارچوب های مرجع نشان داده شده در زیر: استفاده از قاب مرجع نشان داده شده در شکل زیر: قاب اینرسی I (نسبت به مرکز زمین) و قاب غیر اینرسی N (نسبت به یک ناظر در سطح زمین). قاب غیر اینرسی در نتیجه چرخش شتاب می گیرد.
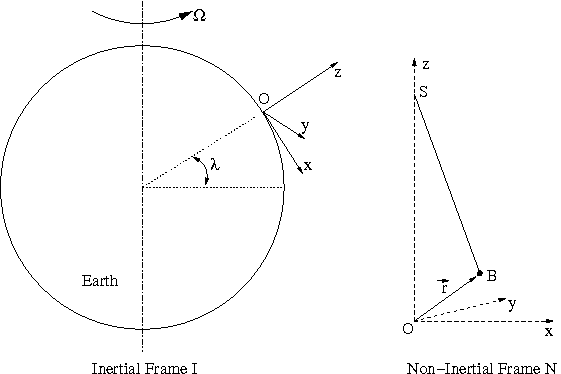
نقطه O مبدا قاب غیر اینرسی N است. این نقطه روی سطح زمین در زیر نقطه تعلیق آونگ می باشد. قاب غیر اینرسی به گونه ای انتخاب می شود که محور z از مرکز زمین دور باشد و بر سطح زمین عمود باشد. محور x به سمت جنوب و محور y به سمت غرب است. همانطور که در مقدمه ذکر شد، صفحه نوسان آونگ فوکو می چرخد. صفحه نوسان یک چرخش کامل را در زمان Trot با فرمول زیر تکمیل می کند، که در آن Tday مدت زمان یک روز است (یعنی زمانی که زمین طول می کشد تا یک بار به دور محور خود بچرخد).
عامل سینوسی نیاز به بحث بیشتر دارد. اغلب به اشتباه فرض می شود که صفحه نوسان آونگ در قاب اینرسی نسبت به مرکز زمین ثابت است. این فقط در قطب شمال و جنوب صادق است. برای از بین بردن این سردرگمی، به نقطه S فکر کنید (شکل بالا را ببینید)، جایی که آونگ معلق است. در قاب اینرسی I، نقطه S روی یک دایره حرکت می کند. باب آونگ روی سیمی با طول ثابت آویزان است. برای سادگی، اصطکاک هوا را نادیده بگیرید. در قاب اینرسی I، تنها دو نیرو وجود دارند که بر روی سطح نوسان می کنند که شامل کشش سیم T و نیروی گرانشی. بردار r موقعیت آونگ را نشان میدهد (قسمت B در شکل بالا را ببینید). قانون دوم نیوتن بیان می کند که مجموع تمام نیروهایی که بر روی یک جسم عمل می کنند برابر با زمان جرمی است.
در سراسر این اثبات ها، نقطه ها بیانگر مشتقات زمانی هستند، فلش ها نشان دهنده بردارها هستند، گپ ها بردارهای واحد را نشان می دهند (i، j، و k در امتداد محورهای x، y، و z). نقطه بالای تیر برداری، مشتق زمانی بردار را نشان می دهد. فلش بالای نقطه بردار نیز مشتق زمان را نشان می دهد. تفاوت بین شتاب کل و شتاب شعاعی را در زیر ببینید.
شتاب کل:
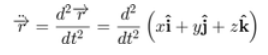
شتاب شعاعی:
شتاب گرانش به سمت مرکز زمین (جهت z منفی).
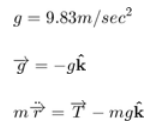
عبارت شتاب را تجزیه کنید:
مشتقات زمانی بردارهای واحد ظاهر می شوند زیرا قاب مرجع غیر اینرسی N در حال چرخش در فضا است. این بدان معناست که بردارهای واحد i، j و k در فضا می چرخند. مشتقات زمانی آنها در زیر آورده شده است. امگا سرعت زاویه ای چرخش زمین به دور محورش است. امگا اسکالر مقدار سرعت زاویه ای است. امگا برداری، بردار سرعت زاویه ای است. جهت آن توسط قانون دست راست تعیین می شود.
مشتق زمانی بردار r را نسبت به امگا بازنویسی کنید.
به همین ترتیب، مشتق زمانی دوم بردار r را بیان کنید.
برای ساده کردن این معادله، فرض کنید که امگا برای زمین بسیار کوچک است. این موضوع به ما امکان می دهد که سومین عبارت را در معادله بالا نادیده بگیریم. در واقع، عبارت دوم (که در حال حاضر بسیار کوچکتر از جمله اول است) چهار مرتبه بزرگتر از عبارت سوم است. این مسئله معادله را به شکل زیر کاهش می دهد:
قانون دوم نیوتن را می توان به صورت زیر نوشت و به اجزای x،y و z تجزیه کرد:
دامنه زاویه ای نوسانات کم است. بنابراین، می توانیم سرعت عمودی و شتاب عمودی (z-dot و z-double-dot) را نادیده بگیریم. اجزای تنش رشته ای را می توان با استفاده از تقریب زاویه کوچک بیان کرد که به طور قابلتوجهی مسئله را ساده می کند و آن را دو بعدی می سازد (شکل زیر را ببینید).
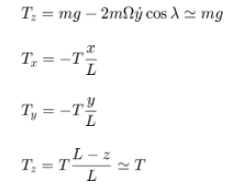
معادلات دیفرانسیل مشخصه
در نهایت فیزیک مساله را می توان با سیستم معادلات کوپل شده زیر توصیف کرد. مختصات x و y موقعیت آونگ را به عنوان ناظر بر روی زمین مشخص می کنند.
راه حل تحلیلی (تقریبی)
در زیر یک راه حل تحلیلی برای مسئله آونگ فوکو ارائه شده که متاسفانه دقیق نیست. اگر بخواهید جواب تحلیلی را با معادلات دیفرانسیل جایگزین کنید، عبارت های لغو نشده مرتبه امگا مربع باقی می مانند. با این حال، از آنجایی که امگا بسیار کوچک است، می توانیم شرایط لغو نشده را برای اهداف عملی نادیده بگیریم.
سیستم معادلات دیفرانسیل واقعی نامتقارن
در طول مشتق، اصطلاحات مربوط به امگا مربع نادیده گرفته شدند. این موضوع منجر به تقارن xy در معادلات دیفرانسیل شد. اگر عبارات مربع امگا در نظر گرفته شوند، سیستم معادلات دیفرانسیل نامتقارن می شود (به فرمول زیر مراجعه کنید).
شما به راحتی می توانید مدل آونگ فوکو فعلی را برای محاسبه معادلات دیفرانسیل نامتقارن تغییر دهید. به سادگی بلوک های Gain مربوطه را که حاوی g/L هستند ویرایش کنید و عبارت لازم را اضافه کنید. این تغییر یک تصحیح کلی بسیار کوچک در نتیجه عددی ایجاد می کند.
نکته پایانی: این مقاله آموزشی MATLAB از مثال های آماده خود نرم افزار MATLAB است که اگر تولباکس سیمولینک (Simulink) بر روی متلب شما نصب باشد، می توانید با تایپ دستور زیر در پنجره کامند متلب به این مدل دسترسی داشته باشید.
1 | openExample('simulink_general/sldemo_foucaultExample') |
منبع: mathworks
هیچ نظری ثبت نشده است