
آزمون حساسیت مدل لورنز غیرخطی آشوبناک در MATLAB
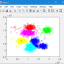
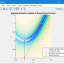
در این بخش پروژه آزمون حساسیت مدل لورنز (Lorenz Model) غیرخطی آشوبناک را در نرم افزار MATLAB آماده کردیم که در ادامه به معرفی پدیده آشوب، مدل های آشوبناک، وجود آشوب در یک سیستم و شناسایی پارامتر های سیستم پرداخته و فیلم و تصاویر خروجی پروژه قرار داده شده است.
پدیده آشوب چیست ؟
نظریه آشوب یا نظریه بی نظمی ها، شاخه ای از ریاضیات است که به مطالعه سیستم های دینامیکی آشفته می پردازد. آشوب پدیده ای است که در اغلب سیستم های غیرخطی تحت شرایط خاصی رخ می دهد. مهم ترین مشخصه در سیستم های آشوبناک حساسیت به شرایط اولیه می باشد. این ویژگی باعث شبیه شدن رفتار این سیستم ها به سیستم های تصادفی می گردد.
مدل های آشوبناک
اما در اصل طبقه بندی این سیستم ها در گروه سیستم های یقینی می باشد. در واقعیت، مدل های آشوبناک بسیاری هستند که از جمله آن ها می توان به مدل های موجود به منظور پیش بینی آب و هوا اشاره نمود. این مدل ها برای اولین بار توسط ادوارد لورنز (Edward Lorenz) معرفی شدند. ادوارد لورنز برای اولین بار پدیده ای به نام آشوب را معرفی نمود و اثر حساسیت به شرایط اولیه را در این سیستم ها مشاهده کرد. حساسیت به شرایط اولیه به این معنی است که در صورتی که سیستم از دو شرط اولیه به اندازه دلخواه، نزدیک به همدیگر شروع به فعالت داشته باشد، پاسخ های سیستم در این دو حالت بعد از گذشت مدتی به طور نمایی از هم فاصله می گیرند. به این نما، نمای لیاپانوف گفته می شود.
وجود آشوب در یک سیستم
برای پی بردن به وجود آشوب در یک سیستم، یکی از راه ها، وجود نمای لیاپانوف مثبت می باشد. نکته مهم در واگرایی پاسخ ها اینجاست که پاسخ های دو سیستم، بی کران نشده و در محدوده خاصی از فضا باقی می مانند. در عمل تمامی یا برخی از پارامتر های موجود در یک سیستم معلوم نیستند. معلوم نبودن پارامترها در یک سیستم آشوبناک با توجه به رفتار آن، مشکلات بسیاری را برای کار با آن سیستم ایجاد می کند.
شناسایی پارامتر های سیستم
روش های مختلفی جهت شناسایی پارامتر های یک سیستم وجود دارد که از آن جمله می توان به روش های مبتنی بر شبکه های عصبی، کنترل تطبیقی، کنترل مقاوم، کمترین مربعات بازگشتی و دیگر روش ها اشاره نمود. در بعضی از روش ها که هدف نهایی در آنها کنترل سیستم می باشد، یافتن مقدار صحیح پارامترها مهم نیست و تنها روشی به منظور تخمین پارامترها استفاده می شود اما در بعضی دیگر روش ها، تخمین های ارائه شده به مقادیر صحیح پارامترها مهم هستند، از این رو نشان دادن این موضوع که تخمین پارامترها به مقادیر صحیح میل می کنند، امری ضروری می باشد.
































هیچ نظری ثبت نشده است