![]()
تخمین ردیابی هدف متحرک با فیلتر کالمن توسعه یافته (EKF) در MATLAB
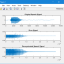
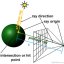
در این بخش پروژه تخمین ردیابی هدف متحرک در محیط سه بعدی با فیلتر کالمن توسعه یافته (Extended Kalman Filter – EKF) را در نرم افزار MATLAB به همراه کامنت گذاری کدها آماده کرده ایم که در ادامه به توضیحاتی از تخمین موقعیت و ردیابی هدف متحرک و فیلتر کالمن پرداخته و فیلم و تصاویر خروجی پروژه در محیط متلب قرار داده شده است.
تخمین موقعیت و ردیابی هدف متحرک
تخمین موقعیت هدف متحرک (Tracking Object) موضوعی مهم در ردیابی است که تاکنون الگوریتم های بسیاری ارائه شده اند. امروزه تلاش های بسیاری در زمینه تشخیص و ردیابی اجسام متحرک از طریق پردازش تصویر انجام شده و الگوریتم های مختلفی نیز در این زمینه طراحی و به صورت سخت افزاری و با استفاده از پردازش سیگنال دیجیتال (DSP) و FPGA پیاده سازی شده اند. با توجه به نوع عملیات و میزان اهمیت دقت و سرعت و … الگوریتم مناسب انتخاب می گردد. ردیابی اهداف بر اساس تعیین موقعیت جسم در فریم های متوالی تصویر انجام می شود. برای ردیابی بلادرنگ اجسام متحرک مانوری همچنین جهت کاهش تاثیر نویز، از روش های بازگشتی تخمین بیزین استفاده می گردد.
تکنیک های تخمین اغلب بر اساس الگوی فیشر یا الگوی بیزین بیان می گردند. در الگوی بیز، پارامتر مجهول تغییر تصادفی دارد و حال آنکه در الگوی فیشر، پارامتر مجهول ثابت می باشد. دیدگاه تئوری بیز در تعیین موقعیت و ردیابی اجسام متحرک، بر اساس تخمین از یک معادله بازگشتی می باشد. تخمین برای سامانه های خطی با نویز گوسی، بر پایه الگوریتم صافی کالمن بیان می گردد و برای سامانه های غیرخطی با نویز گوسی، سامانه قبل از به کار گیری صافی کالمن باید با بسط تیلور مرتبه اول حول بهترین تخمین موجود، خطی شود که این خطی سازی نزدیک حالت تخمین زده، انجام می گیرد و تحت الگوریتم صافی کالمن پیشرفته (EKF) بیان می شود.
اما برای سیستم های غیر خطی به ویژه اگر توزیع نویز نیز غیر گوسی باشد، به جای خطی کردن سامانه جهت استفاده از صافی کالمن، مسئله تخمین را می توان به صورت مستقیم نیز انجام داد و تابع توزیع چگالی احتمال را به صورت عددی و شمارشی بدست آورد. امروزه با رشد روش ها و شیوه های آماری، مسئله تخمین یک پارامتر یا حالت یک سامانه غیر خطی تصادفی در کنار مشاهدات و اندازه گیری های نویزی، توسط تکنیک تخمین مونت کارلو برای مسائل پیچیده آماری انجام می گیرد که در قالب الگوریتم صافی ذره (PF) بیان می گردد.
فیلتر کالمن (Kalman filter)
فیلتر کالمن (Kalman filter) که به عنوان تخمین خطی مرتبه دوم نیز شناخته میشود، الگوریتمی می باشد که حالت یک سیستم پویا را بوسیله مجموعه ای از اندازه گیری های شامل خطا در طول زمان برآورد می کند. فیلتر کالمن اغلب تخمین دقیق تری را نسبت به تخمین بر مبنای یک اندازه گیری واحد بر مبنای استنباط بیزی و تخمین توزیع احتمال مشترکی از یک متغیر تصادفی در یک مقطع زمانی ارائه می کند. فیلتر کالمن (Kalman filter) کاربردهای زیادی در علم و فناوری همچون مسیریابی و پایش وسایل نقلیه، به ویژه هواپیما و فضاپیماها دارد. فیلتر کالمن مفاهیم بسیار وسیعی را در حوزه های سری های زمانی، پردازش سیگنال و اقتصاد سنجی مطرح می سازد.

















 (29 امتیاز از 6 رای)
(29 امتیاز از 6 رای)








هیچ نظری ثبت نشده است